Selten liegen die Daten so vor, wie es ein Optimierungsalgorithmus benötigt. Meist ist eine Vorverarbeitung (Konvertierung, Aggregation, Formatierung) der Input-Daten erforderlich.
Nach der Optimierung müssen die Ergebnisse anschaulich aufbereitet und graphisch dargestellt werden.
Mathematica bietet hierfür eine ideale Arbeitsumgebung mit der erforderlichen Funktionalität.
Da Mathematica eine interaktive und interpretative Arbeitsumgebung ist, erhält der Benutzer laufend Zwischenergebnisse und kann anhand dieser den weiteren Lösungsweg entsprechend einschlagen, der am vielversprechendsten ist.
Ein Beispiel möge zur Verdeutlichung dienen. Die Werte werden hier verkürzt abgedruckt, der Plot zeigt alle Werte.
data = {{0.01, -0.506366}, {0.011, 0.195822}, ..., {0.029, 0.0746909}, {0.03, 0.94053}, {0.031, 0.746068}, ..., {0.1, -0.544021}}
ListPlot[data, Frame -> True, Axes -> False, PlotStyle -> PointSize[0.02]]
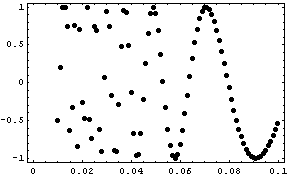
Ist man nun an der Steigung an der Stelle 0.03 interessiert, wird es numerisch schwierig. Einfacher ist es, einen Fit der Daten symbolisch abzuleiten.
fit = Fit[data, {1, Sin[x], Sin[1/x]}, x]
8.38*^-16 + 1.*Sin[1/x] - 1.4*^-14*Sin[x]
fit = Chop[fit]/.{1.0->1}
Sin[1/x]
deriv = D[fit, x]
-Cos[1/x]/x^2
Das Einsetzen des x-Wertes liefert das gewünschte Ergebnis:
deriv/.x->0.03
377.458